Numpy20本ノック
問題その7 四則演算
こちらの行列の四則演算をおこなってください。
上3つの演算にかんしては、なんとなくわかりそうなのですが、
アダマール積ってなに?(笑)
とりあえす、行列を定義します。
足し算と引き算はそのままです。
a= np.array([[1,3],[-2,4]])
b= np.array([[2,-1],[3,0]])
a+b
array([[3, 2],
[1, 4]])
a-b
array([[-1, 4],
[-5, 4]])行列積はすこし違いまして
調べてみると、こんな感じで計算するみたいです。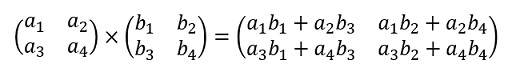
めちゃくちゃ複雑です(笑)
こんな数式どこでつかうんだろう??
たぶん機械学習とかでつかうのかなぁ~(笑)
でこんな複雑な計算もpythonならサクサクッとできます。
書き方も普通に * で計算するわけではなく、
a @ b
もしくは
a.dot(b)
で計算できるそうです。
a= np.array([[-2,-5],[1,3]])
b= np.array([[3,0],[6,-2]])
a @ b
array([[-36, 10],
[ 21, -6]])
a.dot(b)
array([[-36, 10],
[ 21, -6]])アダマール積 とは 要素同士(同じ場所)の掛け算
といういみらしいです。
こちらの方がパッと見わかりやすいです。
a * bで計算できます。
a= np.array([[3,5],[4,-1]])
b= np.array([[-2,1],[0,-3]])
a * b
array([[-6, 5],
[ 0, 3]])問題その8 転置
こちらのベクトル・行列の転置を行ってください。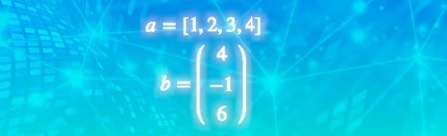
転置は.Tで行えます。
a = np.array([2,3,4])
a
array([2, 3, 4])
a.T
array([2, 3, 4])なにも起こりません。
a = np.array([2,3,4])
だと一次元の値なので、横も縦も定まっていません。
なので一旦[]で囲って二次元の値に変えてから転置を行います。
a = np.array([[2,3,4]])
a = np.array([[2,3,4]])
a
array([[2, 3, 4]])
a.T
array([[2],
[3],
[4]])ここからは、表題の問題と大きく変わってます(笑)
どうゆうわけかわかりませんが、回答動画では
B = np.array([[1.2,3.5,5.1],[-0.3,1.1,-4.5]])
の行列を転置することになります。
B = np.array([[1.2,3.5,5.1],[-0.3,1.1,-4.5]])
B.T
array([[ 1.2, -0.3],
[ 3.5, 1.1],
[ 5.1, -4.5]])


コメント